Cylindrical Coordinates To Spherical Coordinates Calculator

Cylindrical Coordinates To Spherical Coordinates Calculator. Now, let’s look at another example. Articles that describe this calculator.

calculus Change the order of integration in Spherical coordinate and from math.stackexchange.com

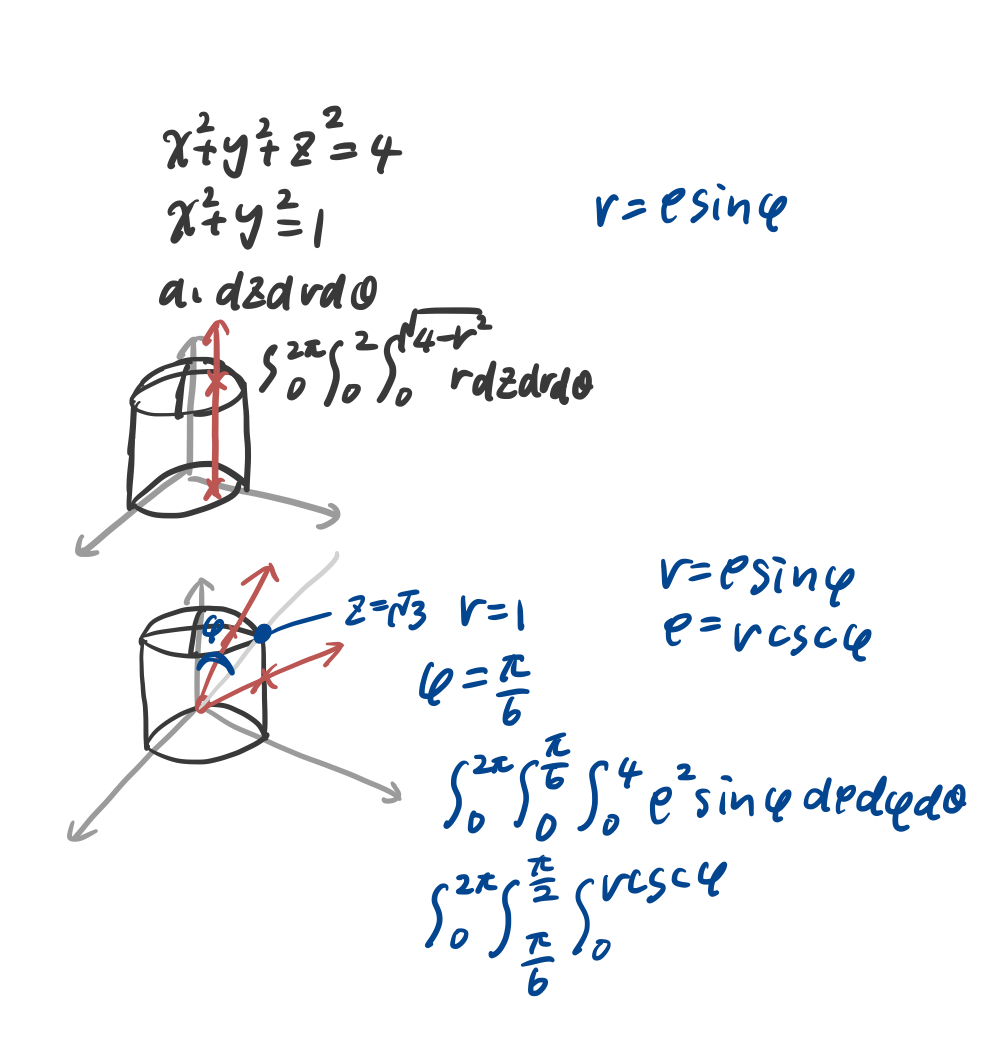
Give the rectangular and cylindrical coordinates for thepoint with spherical coordinates (8, π/2, π).28. Triple integrals in cylindrical and spherical coordinates 5 3. The derivation of these equations is easier if we start transforming from spherical to cylindrical coordinates and then from cylindrical to cartesian coordinates.

Source: sweetsugarcandies-lollipops.blogspot.com

Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Conversion calculator prompting the user to put in cartesian coordinates, which as a result will produce the cylindrical and spherical coordinates with angles in degrees and radians.

Source: www.youtube.com

To improve this 'spherical to cylindrical coordinates calculator', please fill in questionnaire. Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand.

Source: mungfali.com

Use calculator to convert cylindrical to spherical coordinates. Z will will then have a value of 0.

Source: www.youtube.com

And as we have seen for the cylindrical divergence case, the answer could be found in the steps of derivations for divergence in spherical coordinates. I have already explained to you that the derivation for the divergence in polar coordinates i.e.

Source: fdocuments.in

The azimuthal angle is denoted by [,]: You may also change the number of decimal places as needed;

Source: www.tessshebaylo.com

[spherical to cylindrical coordinates] bookmarks. For the given integral, the parameters of the cylindrical coordinates are already given.

Source: www.learningaboutelectronics.com

Z will will then have a value of 0. Shortest distance between two lines.

Source: sites.und.edu

Triple integrals in spherical coordinates if you are studying an object with spherical symmetry, it makes sense to use coordinates to re ect that. However, we will do it much easier if we use our calculator as follows:

Source: www.slideshare.net

To describe the location of a point in space, we need the coordinates.; The calculator converts spherical coordinate value to cartesian or cylindrical one.

Source: www.coursehero.com

This time our goal is to change every r and z into ρ and ϕ while keeping the θ value the same, such that ( r, θ, z) ⇔ ( ρ, θ, ϕ). [cylindrical to spherical coordinates] bookmarks.

Source: math.stackexchange.com

To describe the location of the point on the plane it is necessary to. [cylindrical to spherical coordinates] bookmarks.

Source: www.solitaryroad.com

Now, each variable will be. Spherical and rectangular coordinates convert spherical to cylindrical coordinates using a calculator.

Digits After The Decimal Point:

Shortest distance between two lines. It has to be a positive integer. Plane equation given three points.

I Have Already Explained To You That The Derivation For The Divergence In Polar Coordinates I.e.

Give the rectangular and cylindrical coordinates for thepoint with spherical coordinates (8, π/2, π).28. [spherical to cylindrical coordinates] bookmarks. Note that the angle units of the input and output here are all in radians.

Z = Ρ Cos ( Φ) R = Ρ Sin ( Φ) The Third Component Here Is Θ.

A result will be displayed in a few steps, and you will save yourself a lot of time and trouble. Triple integrals in cylindrical and spherical coordinates 5 3. This tool is very useful in geometry because it is easy to use while extremely helpful to its users.

Note As Well From The Pythagorean Theorem We Also Get, Ρ2 = R2 +Z2 Ρ 2 = R 2 + Z 2.

Now, each variable will be. We can find r and z using the sine and cosine functions respectively: The calculator converts spherical coordinate value to cartesian or cylindrical one.

Now, Let’s Look At Another Example.

So, given a point in spherical coordinates the cylindrical coordinates of the point will be, r = ρsinφ θ = θ z = ρcosφ r = ρ sin φ θ = θ z = ρ cos φ. Use calculator to convert cylindrical to spherical coordinates. We can transform from cartesian coordinates to spherical coordinates using right triangles, trigonometry, and the pythagorean theorem.